进制与零:无即是有
进制的进制
生活中有许多种进制在共同起作用,例如,数学上的十进制、计算机中的二进制、八进制和十六进制、计时的60进制、24进制和7进制。
怎么才能快速地知道1111所对应的具体的进制数值呢?例如,1111对应的二进制、八进制和十六进制是多少?它对应的60进制、24进制和7进制又分别是多少?
因此,为了解决这个问题,科学家们在进制的基础上做了更进一步的抽象。
将每个数字所在的
位单独提取出来。将这些
位并从小到大依次排列。越靠右位数越小,越靠左位数越高。
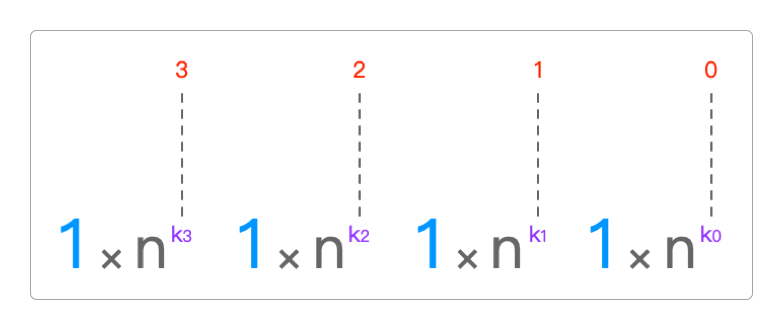
按照这种方式,1111对应的二进制、八进制和十六进制和六十进制就可以这样来表示。
1111分解为二进制的结果。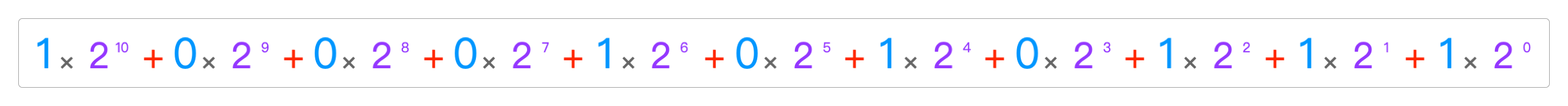
1111分解为二进制的结果 1111分解为八进制的结果。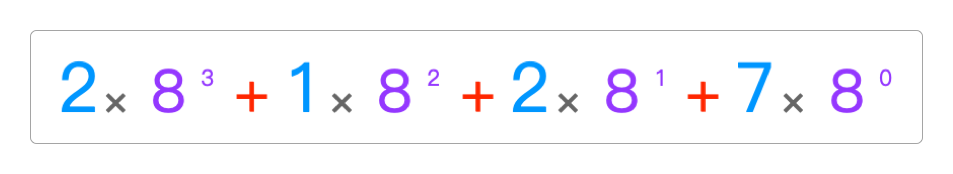
1111分解为八进制的结果 1111分解为十六进制的结果。
1111分解为十六进制的结果 1111分解为六十进制的结果。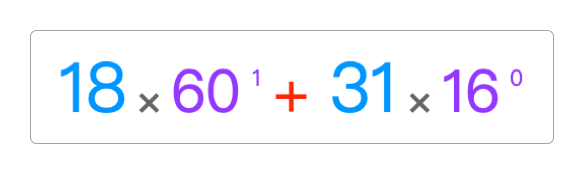
1111分解为六十进制的结果
因此,进制计数法也被称为按位计数法。
0的作用
0在数学上的意义就是没有,但这种没有需要用精确且没有歧义的符号来代表。
例如,如果把101写成1 1,或者将1 1还一不小心被混淆成了11。
所以,0的作用不仅在于替代没有,更重要的是它可以占位:表示某个数位上没有数字。
例如,101就表示它只有百位数、个位数而没有十位数。
这是一种占位的例子。
如果按照没有来算,那

从直觉上来说,0,但如果观察上面幂指数的规律,就可以发现指数每减1,数值就变成了之前的十分之一。
所以,没有。

按照这个规律再继续延伸一下,就可以知道当指数为负数时的结果是什么了。

综合按位计数法与0的意义,就可以得到指数法则。

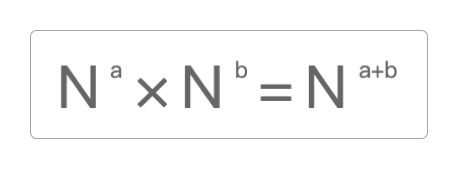
先归纳,再分治
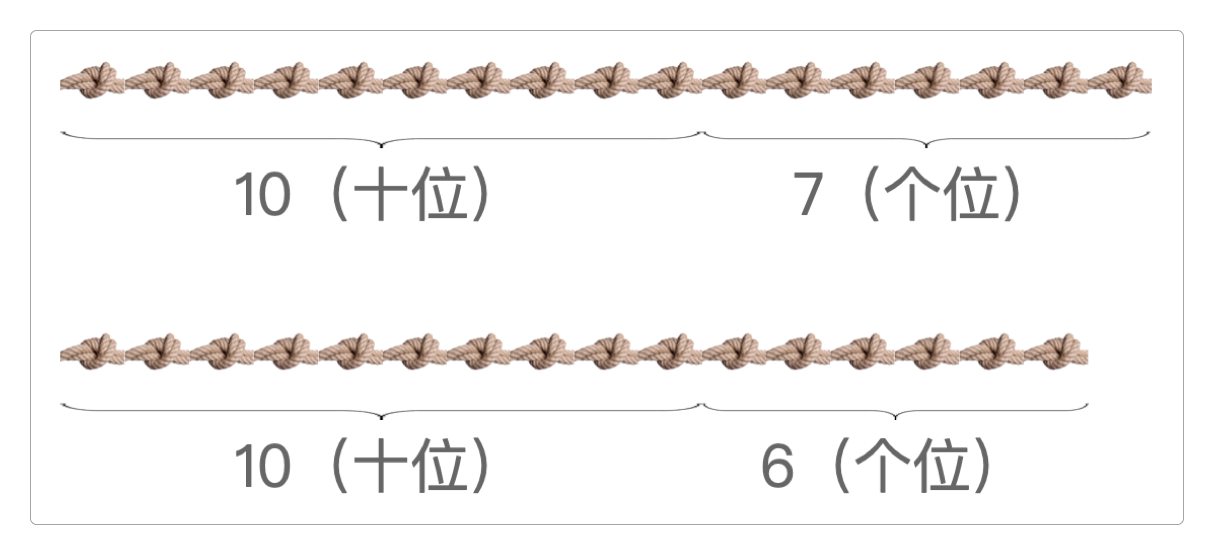
古人用绳结计数,但要记住的事情多了以后,就有点难于表示了。例如,下面两个绳结就不能一眼看出它们的大小(图没画好)。

所以,聪明的先辈们就发明了按位计数法,将大量的数字归纳为一个个小单元,这个小单元就叫位。
以此类推,就有了百位、千位和万位。
但即使这样仍然不能解决数字越来越大的问题。
例如,1111111111111111111和111111111111111111就无法一眼看出它们哪个大,这又回到了绳结比大小的问题。
所以,科学家们想到了指数法则。
1111111111111111111=1.11×111111111111111111=1.11×
好了,这下谁大谁小一目了然了。
按照这种思路,再大的数都可以通不断归纳再分治的方式变得易于管理和识别。
这正是数学的意义。
关注公众号后回复 数学 即可获得程序员的数学栏目剩余文章的访问密码。

