递归：自己定义自己

汉诺塔

GNU全称GNU is Not Unix，这句话当中的第一个GNU又是GNU is Not Unix的英文简写，就这样无穷无尽。

由1883年，法国数学家爱德华·卢卡斯发明了一个名为汉诺塔的游戏。

汉诺塔

它要把套在A圆柱上的圆盘全部移动到B圆柱上，其规则如下。

• 每次只能移动圆柱上最上端的圆盘（将圆盘从一根柱子移到另一根柱子就算移动一次）。

• 小圆盘上不能放大圆盘（也就是要按照A圆柱上已有的次序移过去）。

根据前面学到的分治思想，可以先从圆盘数量少的情况开始尝试解决，然后再用余数思维寻找规律。

7步解决有3个圆盘的汉诺塔

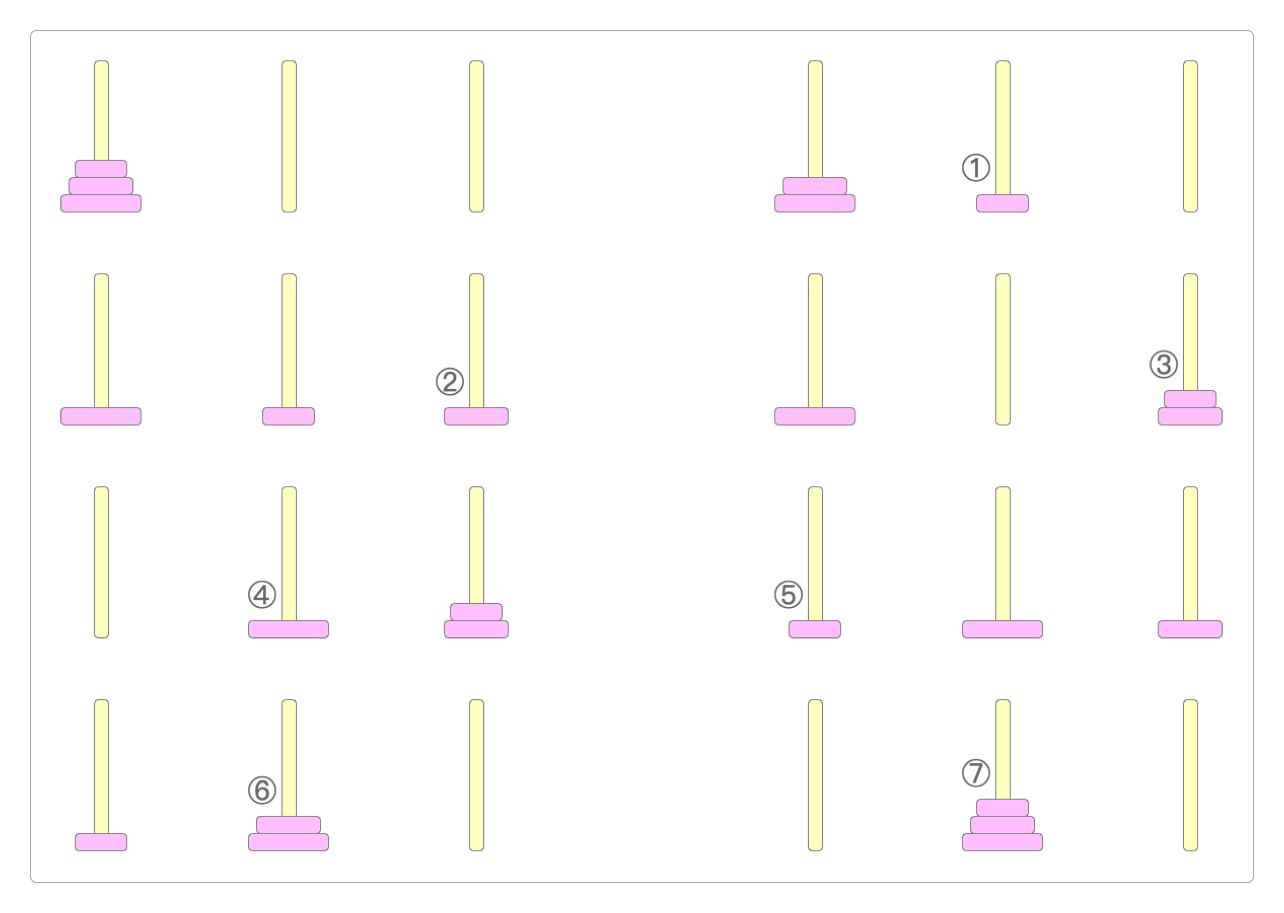
上面的图中用7步解决了只有3个圆盘的汉诺塔。

将圆盘持续增加到4个、5个、6个......发现其中的规律是：要解决n个圆盘的汉诺塔，就需要先解决n-1个圆盘的汉诺塔。

也就是说，利用C柱，将n个圆盘从A柱转移到B柱的通用步骤如下。

• 当n = 0时，什么都不用做。

• 当n > 0时。

  • 首先，将n-1个圆盘从A柱，经由B柱中转，移到C柱（解出n-1层汉诺塔）。

  • 然后，将A柱剩下的最后一个圆盘从A柱移到B柱。

  • 最后，将n-1个圆盘从C柱经由A柱中转，移到B柱（解出n-1层汉诺塔）。

所以，求解n个圆盘的汉诺塔问题可以用公式表示如下。

• H(n) = 0（n=0时）。

• H(n) = H(n - 1) + 1 + H(n - 1)（n=1,2,3......时），这种公式称之为递推公式。

最终得到公式：$H(n)=2^n-1$。

将数字8带进去，得到8个圆盘的汉诺塔要移动圆盘255次才能解决。

因此，对于汉诺塔而言，其本质上就是将n层结构转换为n-1层层的问题，即在求解问题中找出递归结构，并根据它来建立递归公式，将问题抽丝剥茧，逐一解决。

---

感谢支持

更多内容，请移步《超级个体》。