余数：周期性与分组

添码座原创大约 8 分钟

除法即分组

奇数本质上就是被2除余1的数，而偶数是可以被2整除的数。所以，除法其实起到了将数字进行分组的作用。

通过这种思想，可以解决一些比较棘手的问题。

例如，如果今天是星期一，想知道300天以后是星期几该怎么办？

之前说过，星期其实是七进制数在起作用。所以，每过7天，就会得到相同的星期数。

如果今天是周一，那么7天后、14天后、21天后、......294天后，仍然是周一，所以，结论是下面这样的。

294天后是周一 -> 295天后是周二 -> 296天后是周三 -> 297天后是周四 -> 298天后是周五 -> 299天后是周六 -> 300天后是周日

300这个数字并不算大，可以花点时间数过来，但如果要问一万年后的今天是周几该怎么办？

这时候就要用到余数了（假设不考虑闰年，每年按365天算）：365 × 10000 % 7 = 4。

现在能马上知道一万年后是周一之后的4天，也就是周五。

现在问题暂时解决了。

但如同在进制与零中说过的，数字总是会越来越大的——如果现在要知道10¹⁰⁰天之后是周几，又该怎么算呢？

因为这个数太大，用计算机来算都很费力。

通常，在没有办法的时候只能用最笨的办法：一个个地试。所以先尝试用7来对前面几个数求余，看看是否有规律可循。

从结果可以看出：每增加6个0，余数就循环一次。为什么是每6个而不是7个？因为7又回到了自身。

因此，想要计算10¹⁰⁰天之后是周几，就变得比较简单了：100 % 6 = 4。

也就是说，如果今天是周一，那么10¹⁰⁰天之后是周五。

其实这种方法还可以扩展到一切使用进制来计数的地方，例如，现在是早上08:00，10¹⁰⁰个小时后是几点呢？

只不过因为小时是24进制的，所以找规律会麻烦一点，但原理是一样的。

乘方的尾巴

按照上面那种规律，该怎么求123456789^987654321的最后一个数呢？

123456789⁰ 的结果是1，个位数是1
123456789¹ 的结果是123456789，的个位数是9
123456789² 的结果是15241578750190521，的个位数是1
123456789³ 的结果是1881676371789154860897069，的个位数是9
123456789⁴ 的结果是232305722798259244150093798251441，的个位数是1
123456789⁵ 的结果是28679718602997181072337614380936720482949，的个位数是9
......

现在应该看出规律了吧：偶数次方时个位数是1，奇数次方时个位数是9。

由于计算值太大，不得已找了目前对大数计算比较友好的语言Groovy来实现。

黑白棋通信

一位魔术表演者的面前有七枚随机摆放的黑白棋（有的黑面在上，有的白面在上）。

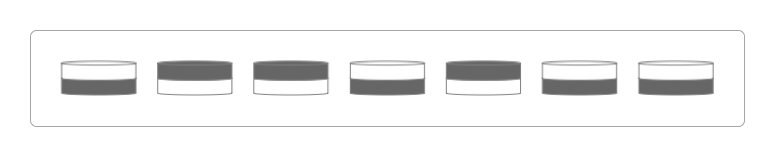
魔术师看完棋子的摆放后就蒙上眼睛，他的徒弟又往里面添加了一枚棋子。

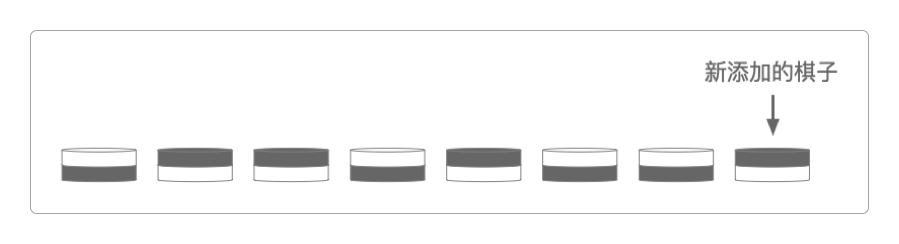
这时观众可以将其中的一枚棋子翻面，或不翻转任何棋子（一次最多只能翻一枚）。

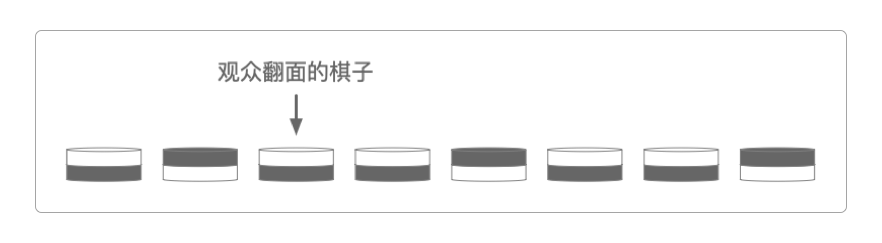
观众翻面时，没有人说话或发出响声，所以魔术师是不知道观众有没有翻棋的。

当魔术师摘下眼罩，观察8枚棋子之后，就能马上知道“观众翻转了棋子”，或者“观众没有翻转棋子”。

这是怎么做到的呢？

其实答案就出在徒弟添加的那枚棋子上。

在魔术师蒙上眼睛之前，可以知道黑棋的个数是奇数还是偶数。
假设徒弟和魔术师约定：添加的棋子，必须让黑棋的个数是偶数。
那么观众的行为就可以造成下面三种结果。
- 观众翻转黑棋，那么黑棋的个数就变成了奇数。
- 观众翻转白棋，那么黑棋的个数也还会是奇数。
- 观众什么也不做，那么黑棋的个数还是偶数。

这就是魔术师可以很快判定观众行为的原因。

这其实就是网络上数据传输的奇偶校验规则：徒弟是发送方，魔术师是接收方，而观众则是干扰信号的噪声。

不过，可以很明显地看出这种检验方式的缺陷：如果观众动了2个或2个以上的棋子，就不好判断了。

找朋友

在一个小村子中，有八户人家，编号分别为A~H，各家之间通过村道相连接。

现在需要找到这个村子中的一位和尚。

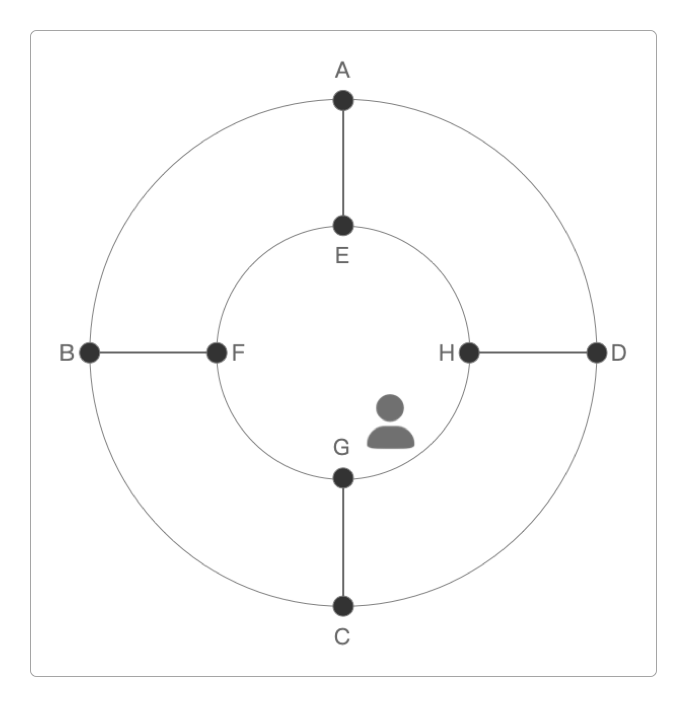
这个和尚住在这八户人家的某一户中，并且他每过一周就会沿着道路去另一家小住（化缘）。

他选择的人家是随机的，无法预测，而且只能沿着村道前进，一次只能前进一格。

现在只知道这位和尚一个半月前住在G这一家中，要算出他目前住在A户的概率。

还是依照惯例，用土办法，先从较小的数开始。

一个半月等于6周。

6周前（移动0次），和尚在G点。
5周前（移动1次），和尚可能在C、F、H其中之一。
4周前（移动2次），和尚可能在B、D、E、G其中之一。
3周前（移动3次），和尚可能在A、C、F、H其中之一。
2周前（移动4次），和尚可能在B、D、E、G其中之一。
1周前（移动5次），和尚可能在A、C、F、H其中之一。
本周（移动6次），和尚可能在B、D、E、G其中之一。

结论：当前和尚并不在A点，所以概率为0。

通过画出他的移动轨迹就可以揭示其中的规律。

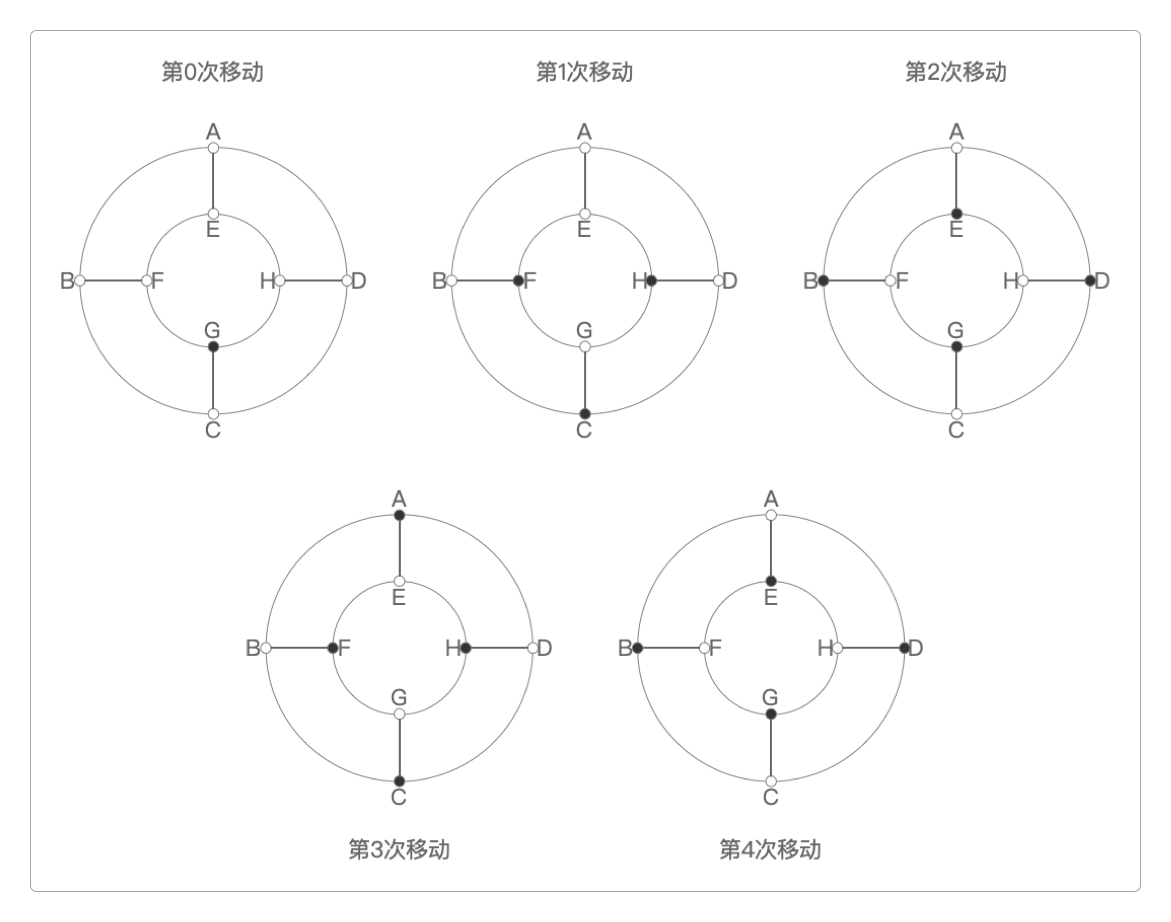
这其中的规律如下。

第奇数次移动后，会出现在A、C、F、H其中之一。
第偶数次移动后，会出现在B、D、E、G其中之一。
A~H要么属于奇数，要么属于偶数，数量各占一半。
A~H没有既属于奇数，又属于偶数的情况。

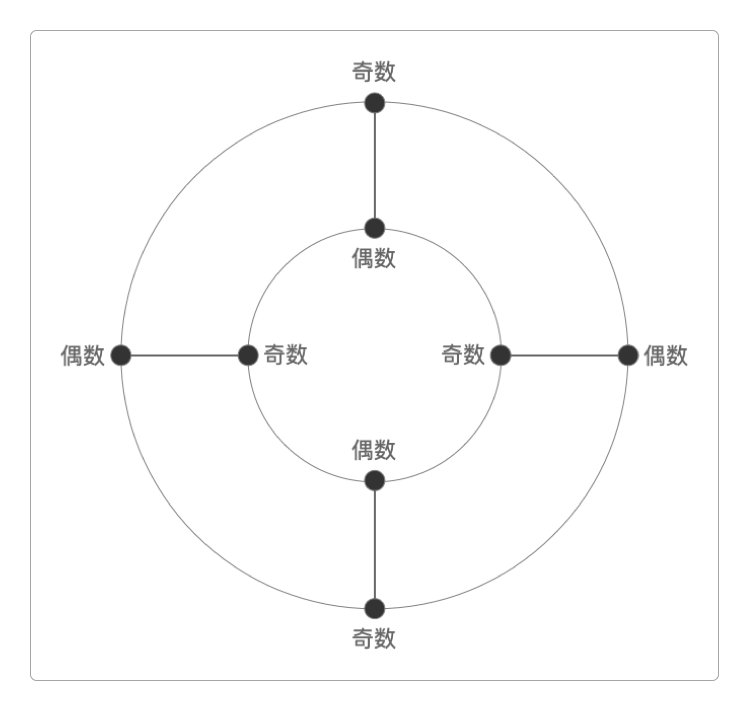
这个问题的启示是：不要挨家挨户地以传统的排列组合来计算概率，而是发现整体的奇偶规律进而得出结论。

柯尼斯堡七桥问题

当现在的加里宁格勒还是当初德国的领土时，在一个叫有柯尼斯堡的小镇，有人提出了这样一个问题。

能不能找到一种方法，一次性经过镇上所有的七座（从a到g）桥呢？

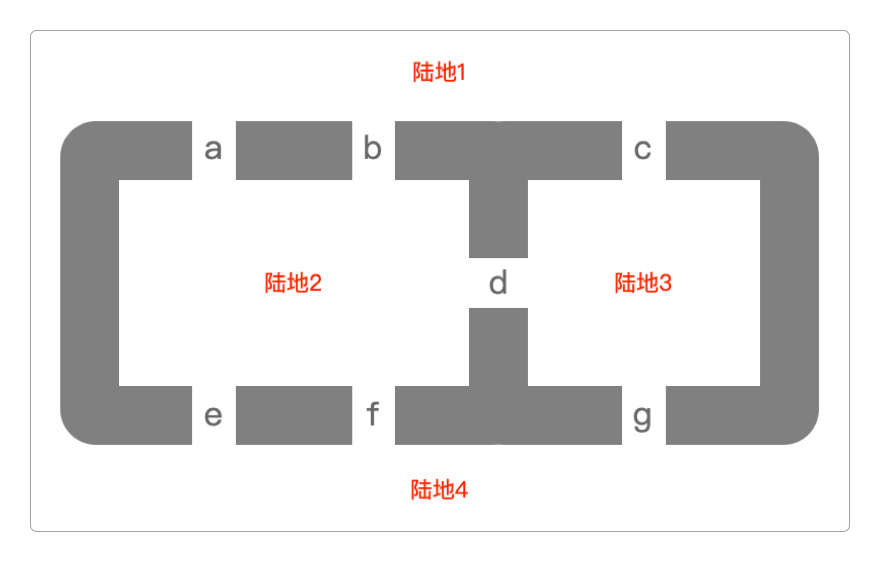
可以从任意一块陆地出发，也可以不回到起点，但必须遵守一个条件：已经走过的桥不能再走。

这就是数学历史上有名的柯尼斯堡七桥问题。

通过这个问题，大数学家欧拉不仅证明了它无解，而且还借此开创了一个新的数学分支：图论。

和数学天才高斯一样，欧拉把这个问题简化成了下面这张图。

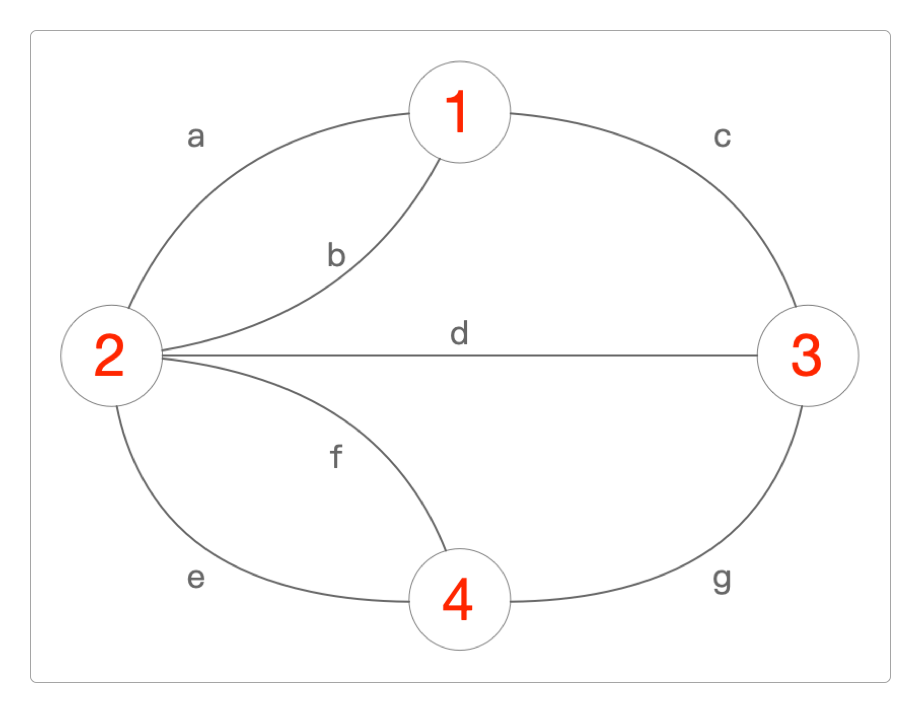
在不断尝试中，欧拉发现，如果要一口气走完七座桥，那么就必须满足下面两个条件之一。

所有的顶点（陆地）的度数（入口和出口的总和）应该为偶数，这是起点和终点相同的情况。
或者，有两个度数为奇数的顶点，其他全是度数为偶数的顶点，这是起点和终点不同的情况。

但从上面的图来看，很明显，这两个条件都不满足。所以欧拉的结论是：不可能一次性走完柯尼斯堡的七座桥。

这是利用数的奇偶性再一次解决具体问题的思维方法。

通过这种方法，就算是镇子上有70座、700座桥也能很快判断它是否走得通。

这种方法也可以扩展到全世界的桥，而不是每遇到一座桥就拿纸拿笔再画一遍。

这就是数学和抽象思维的魅力所在。

感谢支持

更多内容，请移步《超级个体》。