为什么要学它

在人工智能领域中，下面的两类问题会大量用到与微积分相关的数学知识。

• 神经网络中的反向传播算法通过链式求导法则计算各种函数（激活函数、损失函数、优化函数等）对每个权重的偏导数，从而更新网络中的权重。

• 梯度下降则是一种用于寻找函数极值的优化算法，它利用导数的特性来确定问题的优化方向。

通过导数来寻找最优方向

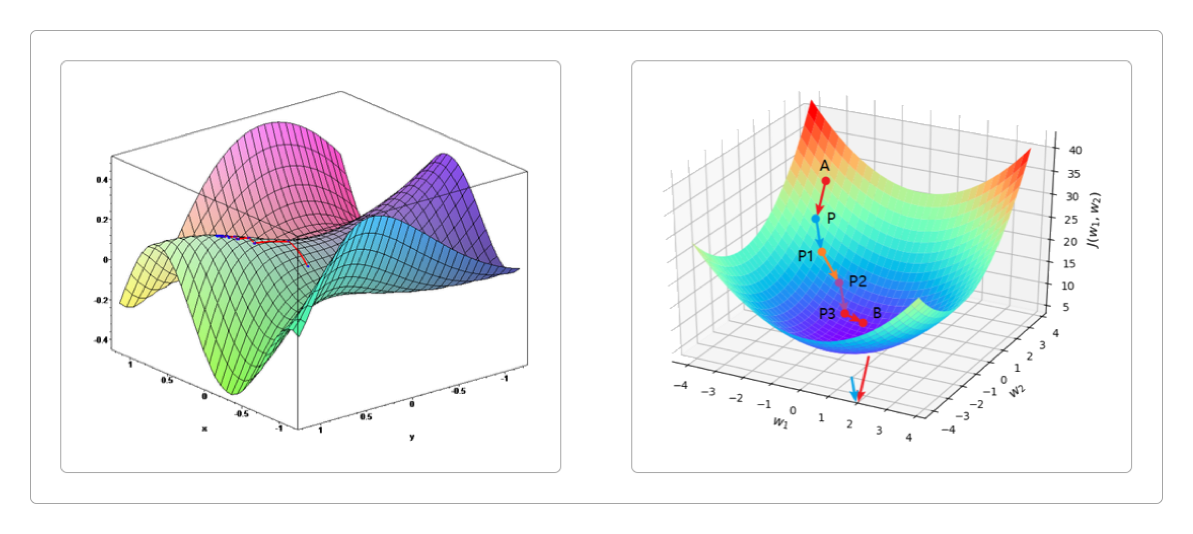
总的来说，微积分主要研究的是当自变量处于极限状态下（无穷大或无穷小）因变量的变化规律问题，以及各种微分方程的应用。

微积分的基本思想是以直代曲和线性近似，将复杂分解为简单，将多元分解为一元，在对结果没有本质影响的前提下，直至找到某一近似的办法来解决它。

高等数学中的集合、映射、函数、多元函数、极限、导数，以及牛顿-莱布尼兹公式、泰勒公式、洛必达法则、拉格朗日中值定理、柯西中值定理、欧拉-麦克劳林求和公式等知识，共同构成了整个微积分的基础，也是后续解决线性代数和概率论中数学问题的主要工具。

上面这些东西看起来非常复杂，但很多都是一脉相承的。

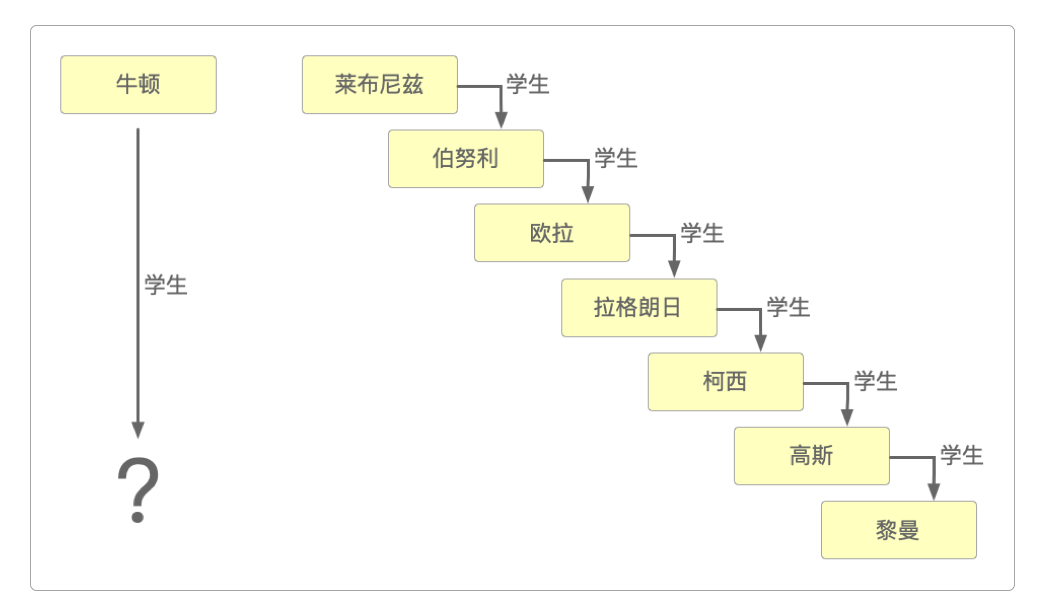
因为艾萨克·牛顿虽然在科学界大名鼎鼎，也是现代微积分的奠基人和经典力学的开创者，但比起戈特弗里德·莱布尼茨对传道授业的热情和对科学人才上的培养上，显然是稍逊风骚的。

人类群星闪耀时

---

关注公众号后回复 高数 即可获得高等数学栏目剩余文章的访问密码。