积分定律

不定积分

在某个定义区间上，如果$F^{\prime }(x)=f(x)$或$\mathrm{d}F(x)=f(x)\mathrm{d}x$，则称$F(x)$为$f(x)$的一个原函数。

函数$f(x)$带有任意常数项的原函数称为$f(x)$的不定积分，记为$\int f(x)\mathrm{d}x$。也就是说，带有任意常数项的原函数$F(x)+C$求导之后就变成了$\int f(x)\mathrm{d}x$。

• 第一类换元积分：令$u=\phi (x),\mathrm{d}u={\phi }^{\prime }(x)\mathrm{d}x$，则$\int f[\phi (x)]{\phi }^{\prime }(x)\mathrm{d}x=[\int f(u)\mathrm{d}u{]}_{u=\phi (x)}$。

• 第二类换元积分：令$x=\phi (t)$单调可导，$\phi (t)\ne 0,\int f[\phi (t)]{\phi }^{\prime }(t)$具有原函数，则$\int f(x)\mathrm{d}x=[\int f[\phi (t)]{\phi }^{\prime }(t)\mathrm{d}t{]}_{t={\phi }^{-1}(x)}$。

定积分

• 函数$f(x)$在$[a,b]$上有界，在$[a,b]$上任意插入若干分点$a=x_0<x_1<x_2<...<x_n=b$。

• 它们把区间$[a,b]$分成$n$个小区间$[x_0,x_1],[x_1,x_2],...,[x_{n-1},x_n]$。

• 每个小区间的长度$\mathrm{\Delta }{x}_1=x_1-x_0,\mathrm{\Delta }{x}_2=x_2-x_1,...,\mathrm{\Delta }{x}_n=x_n-x_{n-1}$，$\lambda =max(\mathrm{\Delta }{x}_1,\mathrm{\Delta }{x}_2,...,\mathrm{\Delta }{x}_n)$。

• 在每个小区间$[x_{i-1},x_i]$上任取一点${\alpha }_i(x_{i-1}\le {\alpha }_i\le x_i)$。

• 若当$\lambda \to 0$时，极限$\underset{\lambda \to 0}{lim}\sum _{i=1}^{n}f({\alpha }_i)\mathrm{\Delta }{x}_i$总存在，且与闭区间$[a,b]$的分法及点${\alpha }_i$的取法无关，则称该极限为函数$f(x)$在区间$[a,b]$上的定积分（简称积分），记作${\int }_a^{b}f(x)\mathrm{d}x$，即${\int }_a^{b}f(x)\mathrm{d}x=\underset{\lambda \to 0}{lim}\sum _{i=1}^{n}f({\alpha }_i)\mathrm{\Delta }{x}_i$。

定积分的几何意义非常明确：就是用来计算面积的。

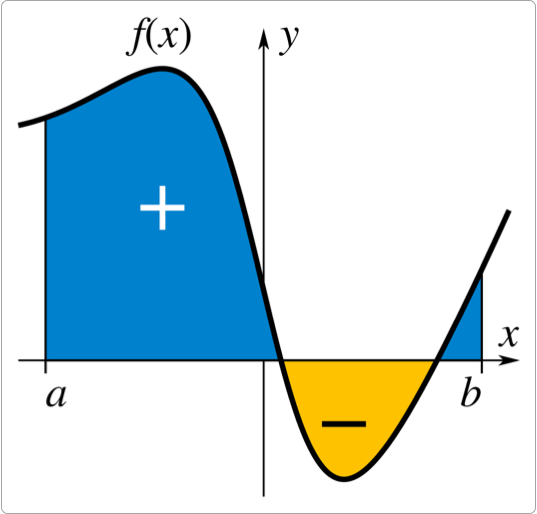定积分的几何意义

定积分中值定理：若$f(x)$在区间$[a,b]$上连续，则在$[a,b]$上至少存在一点$\alpha$，满足${\int }_a^{b}f(x)\mathrm{d}x=f(\alpha )(b-a)$。

牛顿-莱布尼茨公式

如果函数$f(x)$在区间$[a,b]$上连续，则积分上限函数$\mathrm{\Phi }(x)={\int }_a^{x}f(t)\mathrm{d}t$在区间$[a,b]$上可导，且${\mathrm{\Phi }}^{\prime }(x)={\displaystyle \frac{\mathrm{d}}{\mathrm{d}x}}{\int }_a^{x}f(t)\mathrm{d}t=f(x)(a\le x\le b)$，$\mathrm{\Phi }(x)$是$f(x)$的一个原函数，这就是微积分第一基本定理。

如果函数$F(x)$是连续函数$f(x)$在区间$[a,b]$上的一个原函数，则有${\int }_a^{b}f(x)\mathrm{d}x=F(b)-F(a)=F(x){|}_a^b$，这就是微积分第二基本定理，又称为牛顿-莱布尼茨公式。

---

感谢支持

更多内容，请移步《超级个体》。