一元函数的导数与微分

导数的意义

导数的本质是反映割线经过某一点时其斜率的变化情况：${\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}}={\displaystyle \frac{f(x+h)-f(x)}{h}}$。

人类群星闪耀时

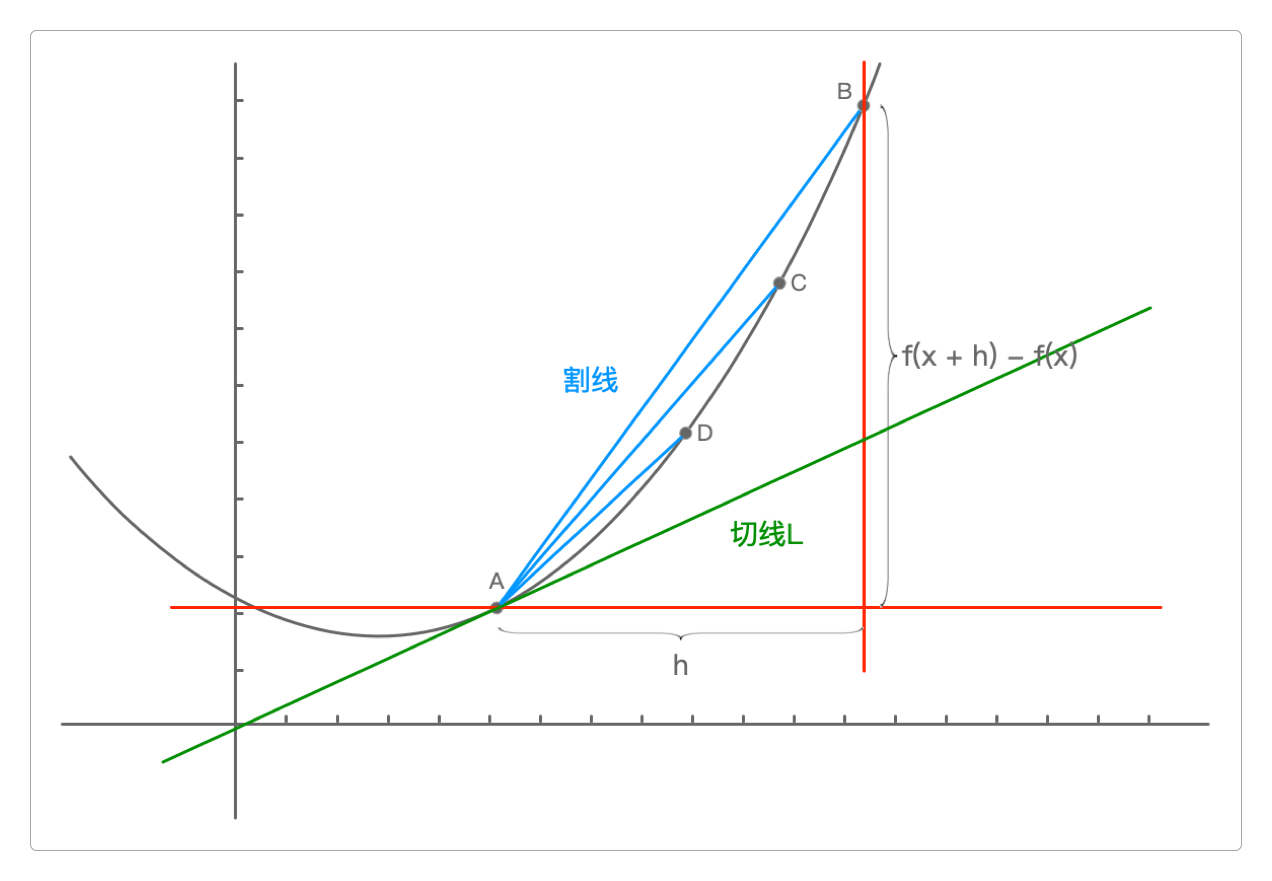
当割线从AB到AC再到AD不断减小，直到AD两点重合之后，就成了切线。

切线L的斜率是$\underset{h\to 0}{lim}={\displaystyle \frac{f(x+h)-f(x)}{h}}$，它表明斜率的绝对值越大，割线越陡峭，$f(x)$函数值的变化也越剧烈。

也就是说，导数反映的是函数$f(x)$的变化趋势，这类似于加速度之于速度的关系。

• 割线反映的是平均速度。

• 切线反映的是瞬时速度。

由于导数的任务是找到一定条件下瞬时速度中的极限（$f^{\prime }(x)=\underset{h\to 0}{lim}={\displaystyle \frac{f(x+h)-f(x)}{h}}$），所以它的主要作用就是用来求解函数的极值和单调性。

另外，导数反映的是变化率或加速度，而一个相对静止或孤立的点是不存在所谓变化量的，例如，折线的转折点就不可导。这就是可导一定连续，连续不一定可导的意义所在。

常用结论和公式

• 当$x\to 0$时, ${\log }_a(1+x)\sim {\displaystyle \frac{1}{{\ln }_a}}x$

• 当$x\to 0$时, $a^x-1\sim {\ln }_{}a·x$

• 当$x\to 0$时, $(1+x{)}^a-1\sim ax$

• 幂函数求导：$(x^n{)}^{\prime }\Rightarrow n·x^{n-1}$。

• 三角函数求导。

  • $(\sin x{)}^{\prime }\Rightarrow \cos x$。

  • $(\cos x{)}^{\prime }\Rightarrow -\sin x$。

• 指数函数求导：$(a^x{)}^{\prime }\Rightarrow a^x{\ln }_{}a$。

• 对数函数求导：$({\log }_{a}x{)}^{\prime }\Rightarrow {\displaystyle \frac{1}{x{\ln }_{}a}}$。

• 函数的和、差、积、商求导。

  • $[\upsilon (x)\pm \nu (x){]}^{\prime }={\upsilon }^{\prime }(x)\pm {\nu }^{\prime }(x)$。

  • $[\upsilon (x)·\nu (x){]}^{\prime }={\upsilon }^{\prime }(x)·\nu (x)+\upsilon (x)·{\nu }^{\prime }(x)$。

  • $[{\displaystyle \frac{\upsilon (x)}{\nu (x)}}{]}^{\prime }={\displaystyle \frac{{\upsilon }^{\prime }(x)·\nu (x)-\upsilon (x)·{\nu }^{\prime }(x)}{{\nu }^2(x)}}$。

• 复合函数求导：$u=g(x)$在点$x$可导，$y=f(u)$在点$u=g(x)$可导，那么${\displaystyle \frac{\mathrm{d}y}{\mathrm{d}x}}={\displaystyle \frac{\mathrm{d}y}{\mathrm{d}u}}·{\displaystyle \frac{\mathrm{d}u}{\mathrm{d}x}}$。

更多求导公式可以参考这里。

微分中值定理

费马定理用于引出罗尔定理，而罗尔定理则用来支持拉格朗日中值定理。

拉格朗日中值定理：如果函数$f(x)$满足以下条件。

• 在闭区间$[a,b]$上连续

• 在开区间$(a,b)$上可导

则$\mathrm{\exists }\xi ,a<\xi <b$，使$f^{\prime }(\xi )={\displaystyle \frac{f(b)-f(a)}{b-a}}$（也就是$f(b)-f(a)=f^{\prime }(\xi )(b-a)$。

拉格朗日中值定理重要意义在于架起了函数与导数之间运算、变换和证明的桥梁。

从几何图形上看，拉格朗日中值定理可以确定：在函数的A、B两点之间一定存在一个点C，使得经过C的切线（也就是它的导数$f(x)$）一定与线段$AB$平行。

拉格朗日中值定理的几何意义

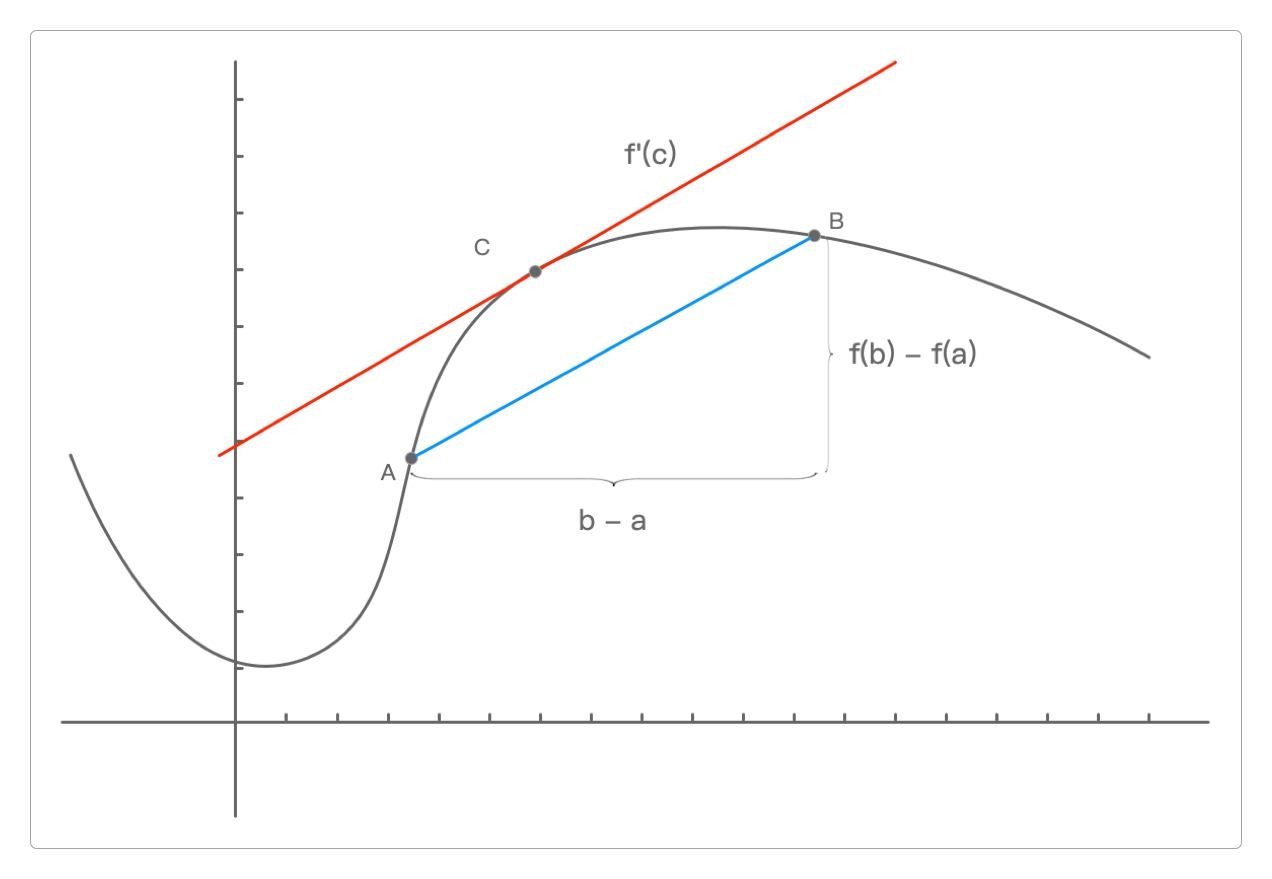
柯西中值定理是拉格朗日中值定理的升级版，只需要知道就可以了，它的几何意义如下图所示。

柯西中值定理的几何意义

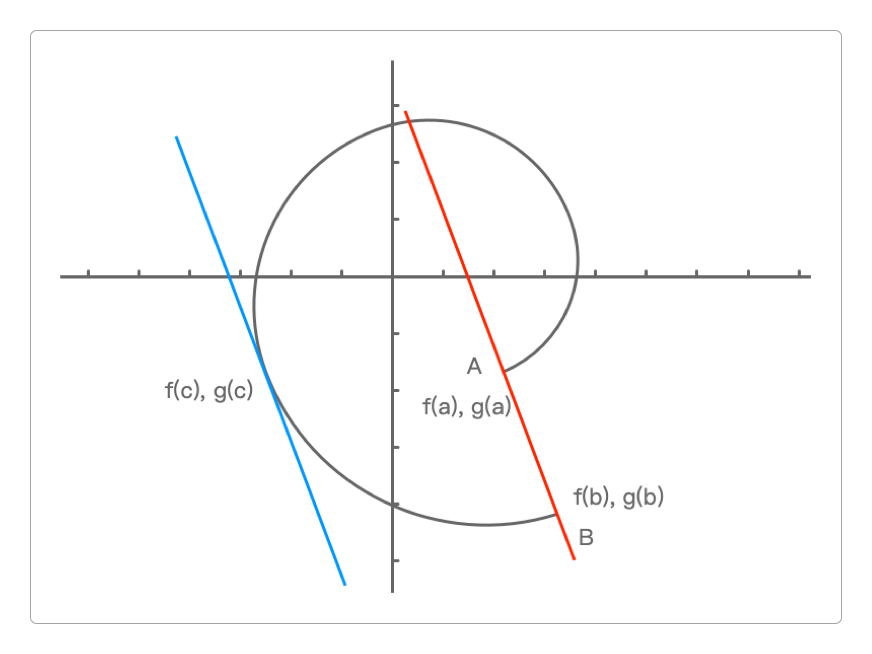
单调性与极值

• 单调性：设函数$f(x)$在闭区间$[a,b]$上连续，在开区间$(a,b)$上可导，在$[a,b]$上取两点$x_1,x_2$满足$a\le x_1\le x_2\le b$，则由拉格朗日中值定理可得如下结论。

  • $f(x_2)-f(x_1)=f^{\prime }(\xi )(x_2-x_1),x_1<\xi <x_2$。

  • 若$x\in (a,b)$时, $f^{\prime }(x)>0$恒成立，则$f(x_2)>f(x_1),f(x)$单调递增。

  • 若$x\in (a,b)$时, $f^{\prime }(x)<0$恒成立，则$f(x_2)<f(x_1),f(x)$单调递减。

• 极值：若函数$f(x)$在点$x_0$有定义，且对于去心邻域$\mathring{U}(x_0)$内的任意$x_1$均满足$f(x)<f(x_0)$（或$f(x)>f(x_0)$），则称$f(x_0)$是函数$f(x)$的一个极大值（或极小值）。

下面是澳门地球物理气象局某一天关于潮汐的曲线图，这是单调性与极值在日常生活中的具体应用。

澳门地球物理气象局

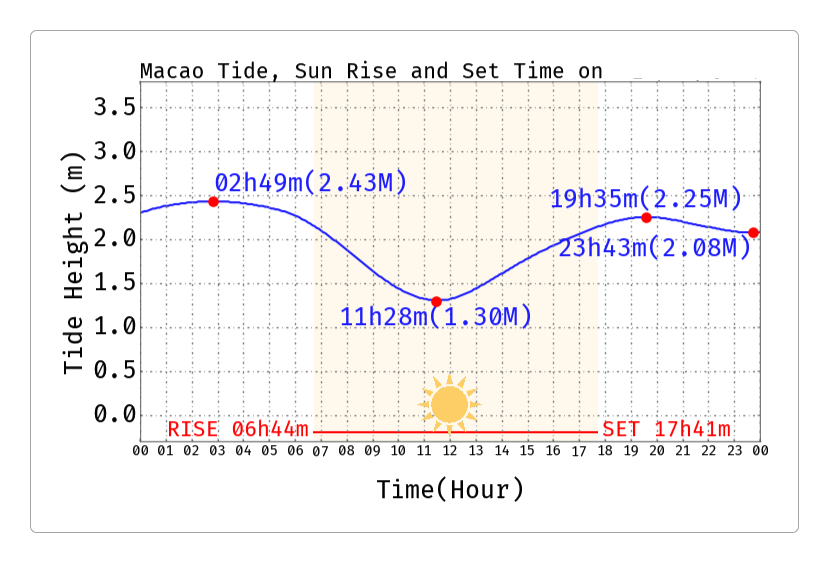
类似这样的例子有无数个，例如，桥梁拱型曲线和承载量的关系，空气升力和飞机表面曲度的关系等，只是平常不引人注意罢了。

凹凸性与拐点

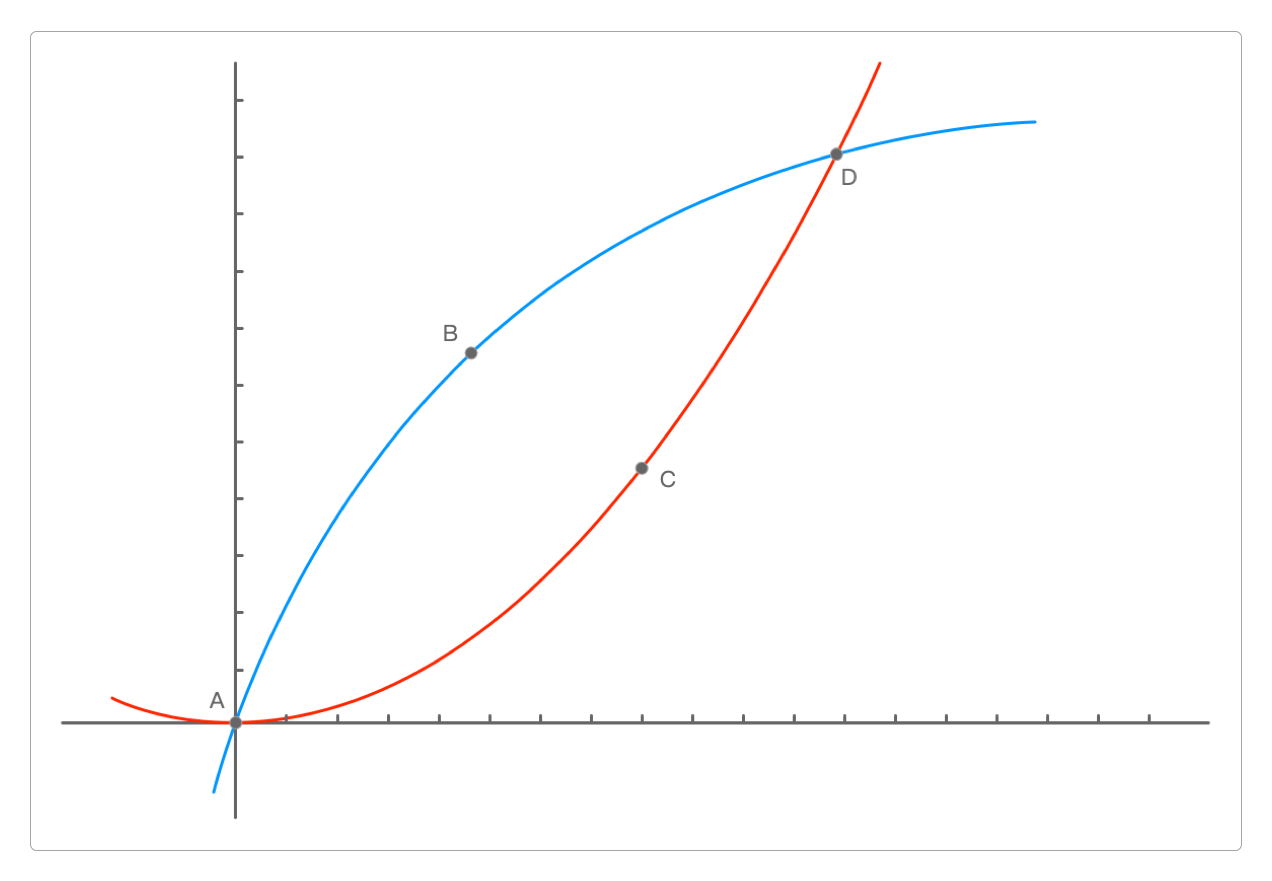
很明显，下图中两条曲线的单调性相同，但凹凸性不同：ABD是凸函数，ACD是凹函数。

同为单调递增，但一个向上凸，一个向上凹

• 设$f(x)$在某区间$U$上连续，若对于$U$上任意两点$x_1,x_2$，恒有$f({\displaystyle \frac{x_1+x_2}{2}})<{\displaystyle \frac{f(x_1)+f(x_2)}{2}}$，则称$f(x)$在$U$上的图形是向上凹的。

• 设$f(x)$在某区间$U$上连续，若对于$U$上任意两点$x_1,x_2$，恒有$f({\displaystyle \frac{x_1+x_2}{2}})>{\displaystyle \frac{f(x_1)+f(x_2)}{2}}$，则称$f(x)$在$U$上的图形是向上凸的。

也可以通过导数来判定函数的凹凸性。

设$f(x)$在某区间$[a,b]$上连续，在$(a,b)$内一、二阶导数均存在。

• 若在$(a,b)$内恒有$f^{″}(x)>0$，则在$[a,b]$上图形是凹的。

• 若在$(a,b)$内恒有$f^{″}(x)<0$，则在$[a,b]$上图形是凸的。

所谓拐点，指的是在某点处左右领域二阶导数异号的点。

洛必达法则

洛必达法则是洛必达花钱买来的，它的主要作用在于解决${\displaystyle \frac{0}{0}}$、${\displaystyle \frac{\mathrm{\infty }}{\mathrm{\infty }}}$、${\displaystyle \frac{0}{\mathrm{\infty }}}$、${\displaystyle \frac{\mathrm{\infty }}{0}}$、${\mathrm{\infty }}^0$、$0^{\mathrm{\infty }}$这一类以往的数学知识无法解决的问题。

令$x_0\in \overline{\mathbb{R}}$（$\overline{\mathbb{R}}$为扩展实数）。

• 设$x\to x_0$时，函数$f(x)\mathrm{和}g(x)$都趋于零，在以$x_0$为端点的去心邻域内可导，且$g^{\prime }(x)\ne 0$，若有$\underset{x\to x_0}{lim}{\displaystyle \frac{f^{\prime }(x)}{g^{\prime }(x)}}$存在或为无穷大，则有$\underset{x\to x_0}{lim}{\displaystyle \frac{f(x)}{g(x)}}=\underset{x\to x_0}{lim}{\displaystyle \frac{f^{\prime }(x)}{g^{\prime }(x)}}$。

• 设$x\to \mathrm{\infty }$时，函数$f(x)\mathrm{和}g(x)$都趋于零，当$|x|>N$时，$f(x)\mathrm{和}g(x)$均可导，且$g^{\prime }(x)\ne 0$，若有$\underset{x\to \mathrm{\infty }}{lim}{\displaystyle \frac{f^{\prime }(x)}{g^{\prime }(x)}}$存在或为无穷大，则有$\underset{x\to \mathrm{\infty }}{lim}{\displaystyle \frac{f(x)}{g(x)}}=\underset{x\to \mathrm{\infty }}{lim}{\displaystyle \frac{f^{\prime }(x)}{g^{\prime }(x)}}$。

此时极限$\underset{x\to x_0}{lim}{\displaystyle \frac{f(x)}{g(x)}}$或$\underset{x\to \mathrm{\infty }}{lim}{\displaystyle \frac{f(x)}{g(x)}}$也被称为未定式。

微分

如果函数的增量$\mathrm{\Delta }y=f(x+\mathrm{\Delta }x)-f(x)$可以表示成$\mathrm{\Delta }y=A·\mathrm{\Delta }x+\circ (\mathrm{\Delta }x)$（A与$\mathrm{\Delta }x$无关），则称函数$f(x)$在点$x$处可微，且$A·\mathrm{\Delta }x$称为相应于$\mathrm{\Delta }y$的微分，记为$\mathrm{d}y$，$\mathrm{d}y=A·\mathrm{\Delta }x$，称$\mathrm{\Delta }x$为微分自变量，记为$\mathrm{d}x$，因此$\mathrm{d}y=A·\mathrm{d}x$。

可微 的充要条件就是 可导 ，这个知道就行了。

微分的数学思想是对变化量进行一种线性近似和逼近，以达到在足够小的范围内可以等价替换的目的。

泰勒公式

泰勒公式的本质就是用多项式来近似地代替某个目标函数。

设$n$是一个正整数。如果定义在一个包含$x_0$的区间上的函数$f(x)$在$x_0$处$n+1$次可导，那么对于这个区间上的任意$x$，都有$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)+{\displaystyle \frac{f^{″}(x_0)}{2!}}+...+{\displaystyle \frac{f^{(n)}(x_0)}{2!}}(x-x_0{)}^n+R_n(x)=\sum _{i=0}^n{\displaystyle \frac{f^{(i)}(x_0)}{i!}}(x-x_0{)}^i+R_n(x)$，其中的多项式$f(x_0)+f^{\prime }(x_0)(x-x_0)+{\displaystyle \frac{f^{″}(x_0)}{2!}}+...+{\displaystyle \frac{f^{(n)}(x_0)}{2!}}(x-x_0{)}^n$（或$\sum _{i=0}^n{\displaystyle \frac{f^{(i)}(x_0)}{i!}}(x-x_0{)}^i$）称为函数$f(x)$在$x_0$处的泰勒级数或泰勒展开式，剩余的$R_n(x)$则称为余项。

从表面来看，泰勒公式非常复杂，但其实它很好理解。这里以$y=sin(x)$举例来说明泰勒公式的意义。

• 一阶导数逼近：$y=x$。

• 三阶导数逼近：$y=x-{\displaystyle \frac{x^3}{3!}}$。

• 五阶导数逼近：$y=x-{\displaystyle \frac{x^3}{3!}}+{\displaystyle \frac{x^5}{5!}}$。

• 七阶导数逼近：$y=x-{\displaystyle \frac{x^3}{3!}}+{\displaystyle \frac{x^5}{5!}}-{\displaystyle \frac{x^7}{7!}}$。

• ......

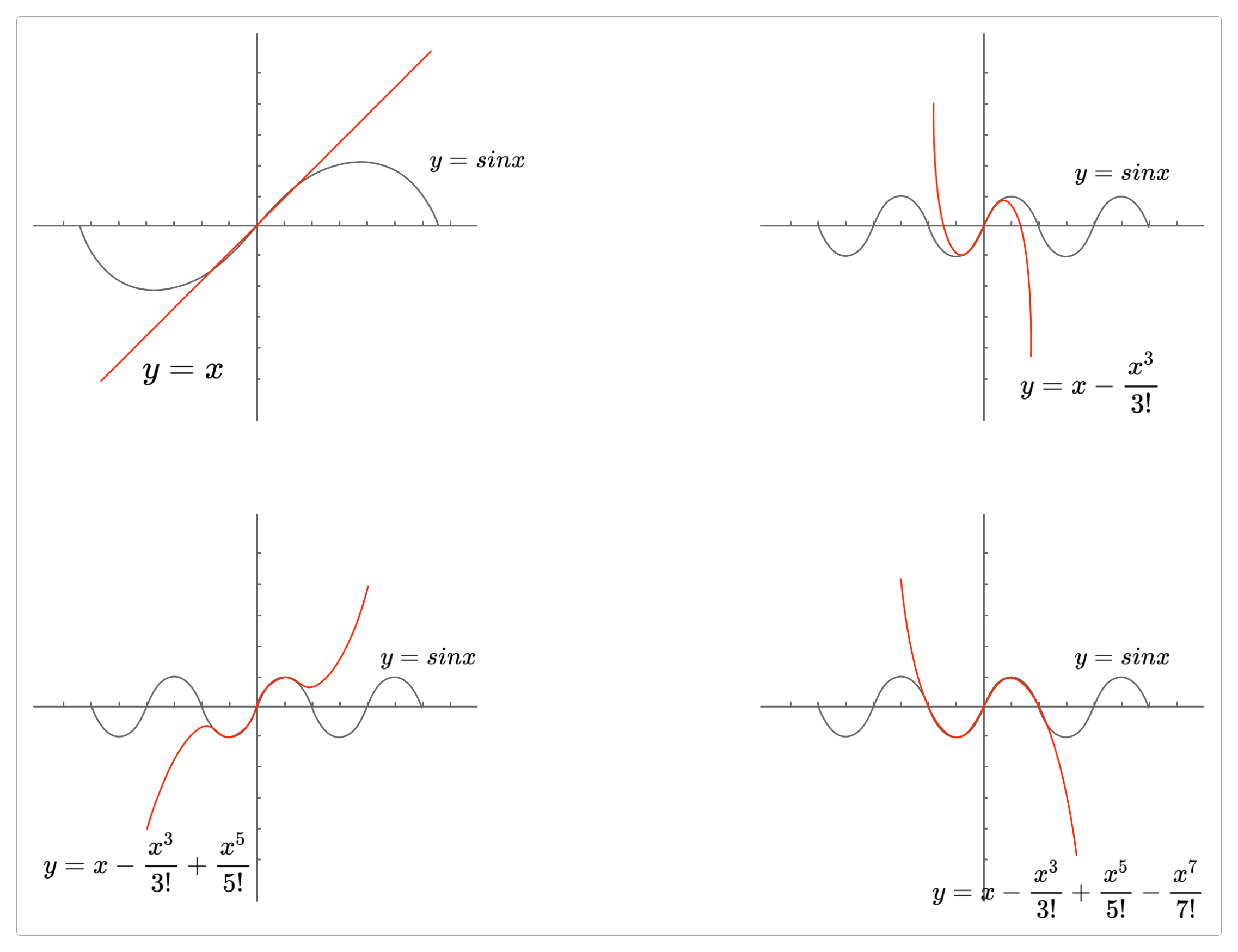
泰勒公式y=sinx的多项式逼近

送上面的图中可以很明显地看到：阶数越高，泰勒公式越接近于原函数$sin(x)$。

泰勒公式有不同类型的余项$R_n(x)$。

• 皮亚诺型余项：当$R_n(x)$是比$(x-x_0{)}^n$更高阶的无穷小时，记作$\circ [(x-x_0{)}^n]$。

• 拉格朗日型余项：当$\xi \in (x_0,x)$时，$R_n(x)={\displaystyle \frac{f^{(n+1)}(\xi )}{(n+1)!}}(x-x_0{)}^{(n+1)}$。

• 积分型余项：$R_n(x)={\int }_{x_0}^x{\displaystyle \frac{f^{(n+1)}(\xi )}{n!}}(x-\xi {)}^n·\mathrm{d}t$。

但并不是随着n的增大，泰勒公式就会无限地逼近目标函数，它存在一个收敛的范围，也就是收敛半径。当超过这个范围时，即使泰勒公式中的项数再多，其逼近的效果也可以忽略不计。

泰勒公式是微积分中非常重要的一个数学公式，它被大量地应用于实际生产中的误差分析和近似替代计算。

---

感谢支持

更多内容，请移步《超级个体》。