多元函数的导数与微分

添码座原创大约 9 分钟

空间方程

若 $\vec{x} = (x_{1}, x_{2}, . . ., x_{n})$ ， $\vec{y} = (y_{1}, y_{2}, . . ., y_{n})$ ， $\vec{x} \in R^{n}$ ， $\vec{y} \in R^{n}$ 。

那么向量的线性运算规则如下。

$\vec{x} \pm \vec{y} = (x_{1} \pm y_{1}, x_{2} \pm y_{2}, . . ., x_{n} \pm y_{n})$ 。
$λ \vec{x} = (λ x_{1}, λ x_{2}, . . ., λ x_{n})$ ， $λ \in R$ 。
向量的模： $| \vec{x} | = (\sqrt{x_{1}^{2} + x_{2}^{2} + . . . + x_{n}^{2}})$ 。
数量积
- $\vec{x} \cdot \vec{y} = (x_{1} y_{1} + x_{2} y_{2} + . . . + x_{n} y_{n})$ 。
- $\vec{x} \cdot \vec{y} = | \vec{x} | \cdot | \vec{y} | \cdot \cos θ$ 。

空间平面方程的一般形式是： $a x + b y + c z + d = 0$ 。

两个平面交线构成的空间直线方程的一般形式是： ${\begin{cases} a_{1} x + b_{1} y + c_{1} z + d_{1} = 0 \\ a_{2} x + b_{2} y + c_{2} z + d_{2} = 0 \end{cases}$

空间曲线参数方程的一般形式是： ${\begin{cases} x = x (t) \\ y = y (t) \\ z = z (t) \end{cases}$

二元函数

设 $D$ 是 $R^{2}$ 上的非空子集，映射 $f : D \to R$ 为定义在 $D$ 上的二元函数，可记为 $z = f (x, y)$ ， $(x, y) \in D$ 。

设二元函数 $f (x, y)$ 的定义域为 $D$ ， $P_{0} (x_{0}, y_{0})$ 是 $D$ 的聚点，如果存在常数 $A$ ，对于任意给定的正数 $ε$ ，总存在正数 $δ$ ，使得当点 $P (x, y) \in D \cap \overset{˚}{U} (P_{0}, δ)$ 时，都有 $lim_{(x, y) \to (x_{0}, y_{0})} f (x, y) = A$ ，则称 $A$ 为函数 $f (x, y)$ 为 $(x, y) \to (x_{0}, y_{0})$ 时的极限，记为 $| f (x, y) - A | < ε$ 。

由于二元函数是空间平面方程中的某一个点，因此它的极限的趋近方向可以有无穷多个。

当任意方向趋近于某点时，函数值都趋近于同一个值，此时的极限才存在。

一切多元初等函数在其定义区间内都是连续的。

一般地，如果 $f (x, y)$ 是初等函数，且 $(x_{0}, y_{0})$ 是函数 $f (x, y)$ 定义域内的点，那么函数 $f (x, y)$ 在点 $(x_{0}, y_{0})$ 处连续，则有 $lim_{(x, y) \to (x_{0}, y_{0})} f (x, y) = f (x_{0}, y_{0})$ 。
在有界闭区间 $D, D \in R$ 上的多元连续函数必然在 $D$ 上有界，且能取得最大值和最小值。
在有界闭区间 $D, D \in R$ 上的多元连续函数必然能取得介于最大值和最小值之间的任何值。

偏导数

设函数 $z = f (x, y)$ 在点 $(x_{0}, y_{0})$ 的某一邻域内有定义。如果 $lim_{Δ x \to 0} \frac{f (x_{0} + Δ x, y_{0}) - f (x_{0}, y_{0})}{Δ x}$ 存在，则该极限为函数 $z = f (x, y)$ 在点 $(x_{0}, y_{0})$ 处的偏导数，记为 $\frac{\partial z}{\partial x} |_{y = y_{0}}^{x = x_{0}}, \frac{\partial f}{\partial x} |_{y = y_{0}}^{x = x_{0}}, z_{x} |_{y = y_{0}}^{x = x_{0}}$ 或 $f_{x} (x_{0}, y_{0})$ 。

若函数 $z = f (x, y)$ 在其定义域内的任意一点 $(x, y)$ 的偏导数均存在，那么这个偏导数就是关于点 $(x, y)$ 的偏导函数。

对 $x$ 的偏导函数记为 $\frac{\partial z}{\partial x}, \frac{\partial f}{\partial x}, z_{x}$ 或 $f_{x} (x, y)$ 。
对 $y$ 的偏导函数记为 $\frac{\partial z}{\partial y}, \frac{\partial f}{\partial y}, z_{y}$ 或 $f_{y} (x, y)$ 。

另外，偏导数的数学符号 $\frac{\partial z}{\partial x}$ 是一个整体，不像一元函数 $\frac{d y}{d x}$ 那样可以视为 $d y$ 和 $d x$ 的商。

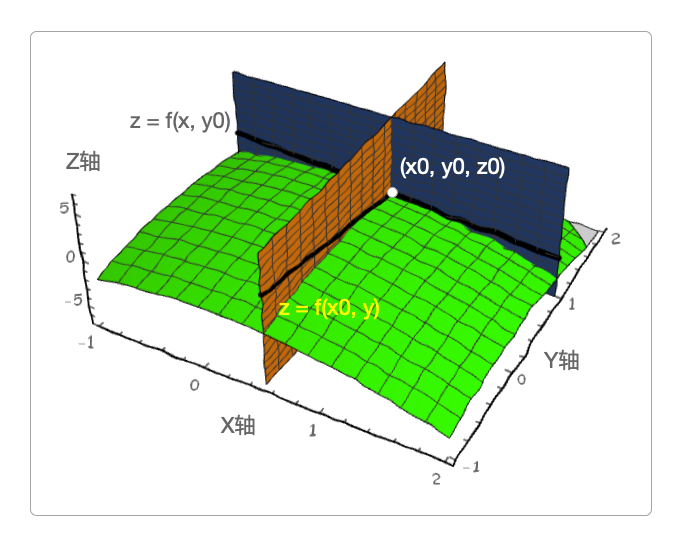
偏导数的几何意义在于求曲线在某个点处的切线对于 $X$ 轴的斜率。

偏导数 $f_{x} (x_{0}, y_{0})$ 表示切面上的某一点 $(x_{0}, y_{0}, z_{0})$ 相对于 $X$ 轴切线的斜率。
偏导数 $f_{y} (x_{0}, y_{0})$ 表示切面上的某一点 $(x_{0}, y_{0}, z_{0})$ 相对于 $Y$ 轴切线的斜率。

极值

极大值：设函数 $z = f (x, y)$ 的定义域为 $D$ ， $P_{0} (x_{0}, y_{0})$ 是 $D$ 的聚点。若存在 $P_{0}$ 的某个邻域 $U (P_{0}) \in D$ ，使得对于该邻域内异于 $P_{0}$ 的任何点 $x, y$ 都有 $f (x, y) < f (x_{0}, y_{0})$ ，则称 $f (x_{0}, y_{0})$ 为函数的极大值。
极小值：设函数 $z = f (x, y)$ 的定义域为 $D$ ， $P_{0} (x_{0}, y_{0})$ 是 $D$ 的聚点。若存在 $P_{0}$ 的某个邻域 $U (P_{0}) \in D$ ，使得对于该邻域内异于 $P_{0}$ 的任何点 $x, y$ 都有 $f (x, y) > f (x_{0}, y_{0})$ ，则称 $f (x_{0}, y_{0})$ 为函数的极小值。

全微分

根据一元函数的微分公式 $Δ y = A \cdot Δ x + \circ (Δ x)$ ，猜想二元函数 $z = f (x, y)$ 的微分公式为： $Δ z = A \cdot Δ x + B \cdot Δ y + \circ (Δ x, Δ y)$ ，并且可以进一步猜想 $A = \frac{\partial f}{\partial x}$ ， $B = \frac{\partial f}{\partial y}$ 。

设函数 $z = f (x, y)$ 在点 $(x, y)$ 的某个邻域内有定义，如果函数在点 $(x, y)$ 的全增量 $Δ z = f (x + Δ x, y + Δ y) - f (x, y)$ 可表示为 $Δ z = A \cdot Δ x + B \cdot Δ y + \circ (ρ), ρ = \sqrt{(Δ x)^{2} + (Δ y)^{2}}$ ，且 $A, B$ 与 $Δ x, Δ y$ 无关，则称函数 $z = f (x, y)$ 在点 $(x, y)$ 可微分， $A \cdot Δ x + B \cdot Δ y$ 称函数在点 $(x, y)$ 处的全微分，记为 $d z = A \cdot Δ x + B \cdot Δ y$ 。

全微分存在的充分条件是：函数 $z = f (x, y)$ 的偏导数在点 $(x, y)$ 处连续。

全微分存在的必要条件是：点 $(x, y)$ 处的偏导数存在，且 $d z = \frac{\partial z}{\partial x} \cdot Δ x + \frac{\partial z}{\partial y} \cdot Δ y$ 。

一元函数中某点的微分表示可以用该点切线逼近的方式来表示该函数。

二元函数中某点的全微分表示可以用该点切面逼近的方式来表示该函数。

方向导数与梯度下降

方向导数和梯度下降是整个微积分中的重点之一，方向导数的意义在于 在变化率最大的方向上寻找函数极值。

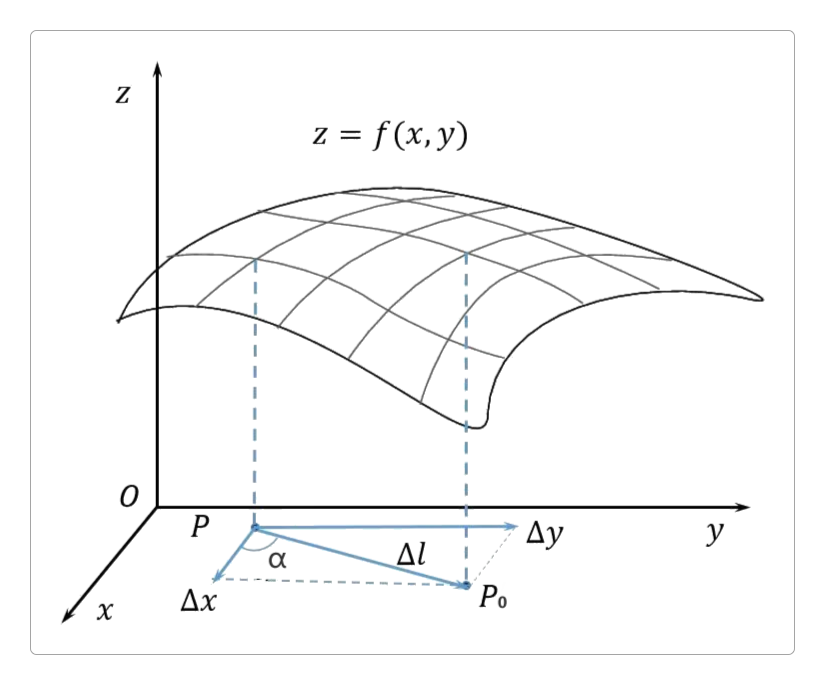
单位方向向量 $\vec{e_{l}} = (\cos α, \cos β)$ ，射线以 $P_{0} (x_{0}, y_{0})$ 为起点，且与 $\vec{e_{l}}$ 同向，则射线的参数方程为 ${\begin{cases} x = x_{0} + t \cdot \cos α \\ y = y_{0} + t \cdot \cos β \end{cases} (t \geq 0)$
函数 $z = f (x, y)$ 在 $P_{0}$ 的某个邻域内有定义， $P_{0}$ 到 $P$ 的函数增量为 $Δ z = f (x_{0} + t \cos α, y_{0} + t \cos β) - f (x_{0}, y_{0})$ ， $P_{0}$ 到 $P$ 的距离为 $| P_{0} P | = \sqrt{(x_{0} + t \cos α - x_{0})^{2} + (y_{0} + t \cos β - y_{0})^{2}} = t$ 。
当 $P$ 沿 $l$ 趋近 $P_{0}$ 时，比值 $\frac{Δ z}{P_{0} P} = \frac{f (x_{0} + t \cos α, y_{0} + t \cos β)}{t}$ 的极限即为方向导数，记为 $\frac{\partial f}{\partial l} |_{(x_{0}, y_{0})} = lim_{t \to 0^{+}} \frac{f (x_{0} + t \cos α, y_{0} + t \cos β) - f (x_{0}, y_{0})}{t} = g (α, β)$ 。

也就是说， $g (α, β)$ 的最大值表示函数在某个方向上具有的最大变化率。

当全微分存在时， $f (x_{0} + t \cos α, y_{0} + t \cos β) - f (x_{0}, y_{0}) = f_{x} (x_{0}, y_{0}) \cdot t \cos α + f_{y} (x_{0}, y_{0}) \cdot t \cos β + \circ (t)$ ，代入方向导数化简得到 $g (α, β) = f_{x} (x_{0}, y_{0}) \cdot \cos α + f_{y} (x_{0}, y_{0}) \cdot \cos β$ 。

记向量 $\vec{a} = (f_{x} (x_{0}, y_{0}), f_{y} (x_{0}, y_{0}))$ ， $\vec{e_{l}} = (\cos α, \cos β)$ ，则有 $g (α, β) = f_{x} (x_{0}, y_{0}) \cdot \cos α + f_{y} (x_{0}, y_{0}) \cdot \cos β = | \vec{a} | \cdot | \vec{e_{l}} | \cdot \cos θ$ ， $θ$ 是向量 $\vec{a}$ 与向量 $\vec{e_{l}}$ 的夹角。

当 $\vec{a}$ 、 $\vec{e_{l}}$ 同向时， $g (α, β)$ 取得最大值 $\sqrt{f_{x}^{2} (x_{0}, y_{0}) + f_{y}^{2} (x_{0}, y_{0})}$ 。
当 $\vec{a}$ 、 $\vec{e_{l}}$ 反向时， $g (α, β)$ 取得最小值 $- \sqrt{f_{x}^{2} (x_{0}, y_{0}) + f_{y}^{2} (x_{0}, y_{0})}$ 。

向量 $\vec{a} = (f_{x} (x_{0}, y_{0}), f_{y} (x_{0}, y_{0}))$ 则被称为梯度，记为 $g r a d f (x_{0}, y_{0})$ 。

梯度指明了函数变化率最大和最小的方向。

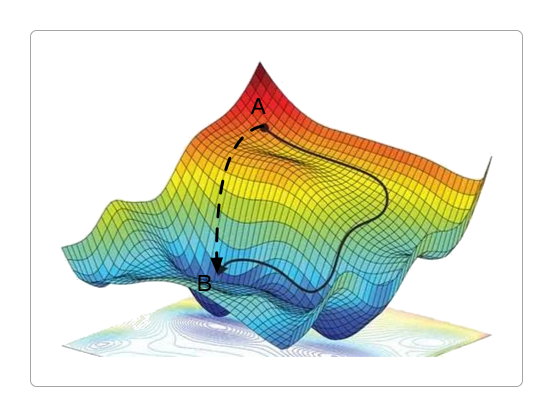
需要注意的是：梯度下降并不是全局变化最快的，而是局部最快。

显然，从全局角度来说，从点 $A$ 到点 $B$ 应该是虚线最快，但实际计算结果可能会有一定的随机性，例如，上图中的结果是沿着实线的方向进行迭代。

通过Python演示梯度下降算法。

# 用梯度下降算法求函数最小值：z = x^2 + 2y^2
import matplotlib.pyplot as plt

# 搜索步长
m = 0.01
x = -10
y = 30
L = x ** 2 + 2 * y ** 2
# 迭代次数
n = 0
# 迭代误差
err = 1
# 迭代阈值
threshold = 0.0000001
value = []

while (err > threshold) and n < 100:
    # 迭代
    x = x - 2 * m * x
    y = y - 4 * m * y
    # 计算前后两次迭代后函数差值的绝对值
    err = abs(x ** 2 + 2 * y ** 2 - L)
    value.append(err)
    L = x ** 2 + 2 * y ** 2
    # print(x, y, n)
    n = n + 1
print(x, y, L, n)
plt.plot(value)
plt.show()

感谢支持

更多内容，请移步《超级个体》。