线性回归

添码座原创大约 3 分钟

数据之间的关系可以由具体参数未知的某种函数或者方程来近似地表示，求得这些未知参数的方式就被称为拟合。

用简单的大白话来说就是用曲线来串联起采样或实验过程中得到的若干离散数据点，然后再用方程来表示它们，以求得更一般的规律。

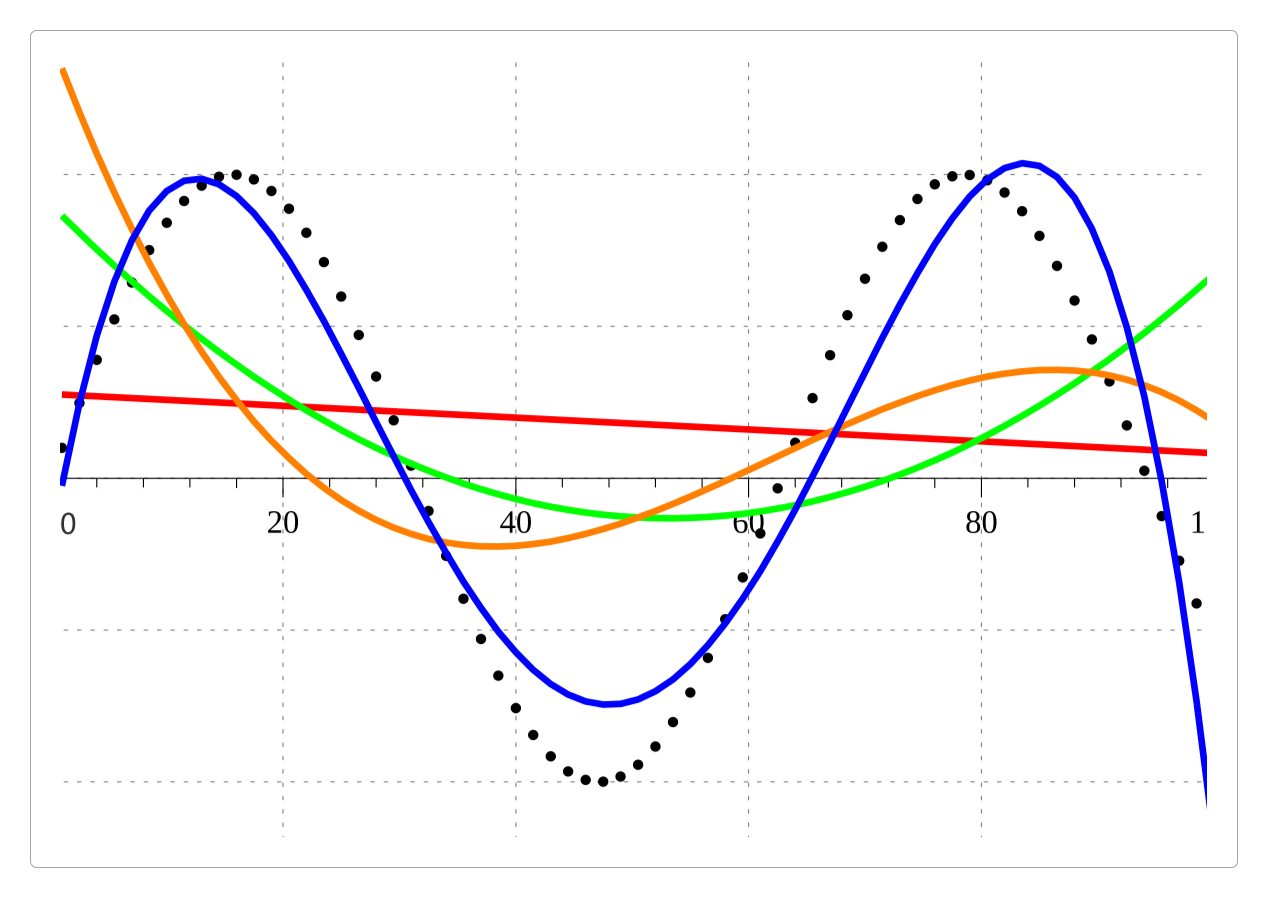
在上面的图中，黑色的点为原始采样数据。

红色曲线：一次多项式。
绿色曲线：二次多项式。
橙色曲线：三次多项式。
蓝色曲线：四次多项式。

可以看到，多项式的次数越多，拟合效果越好。

当采样数据呈现出线性关系时，这种拟合的方式也可以称之为回归（或线性回归）。

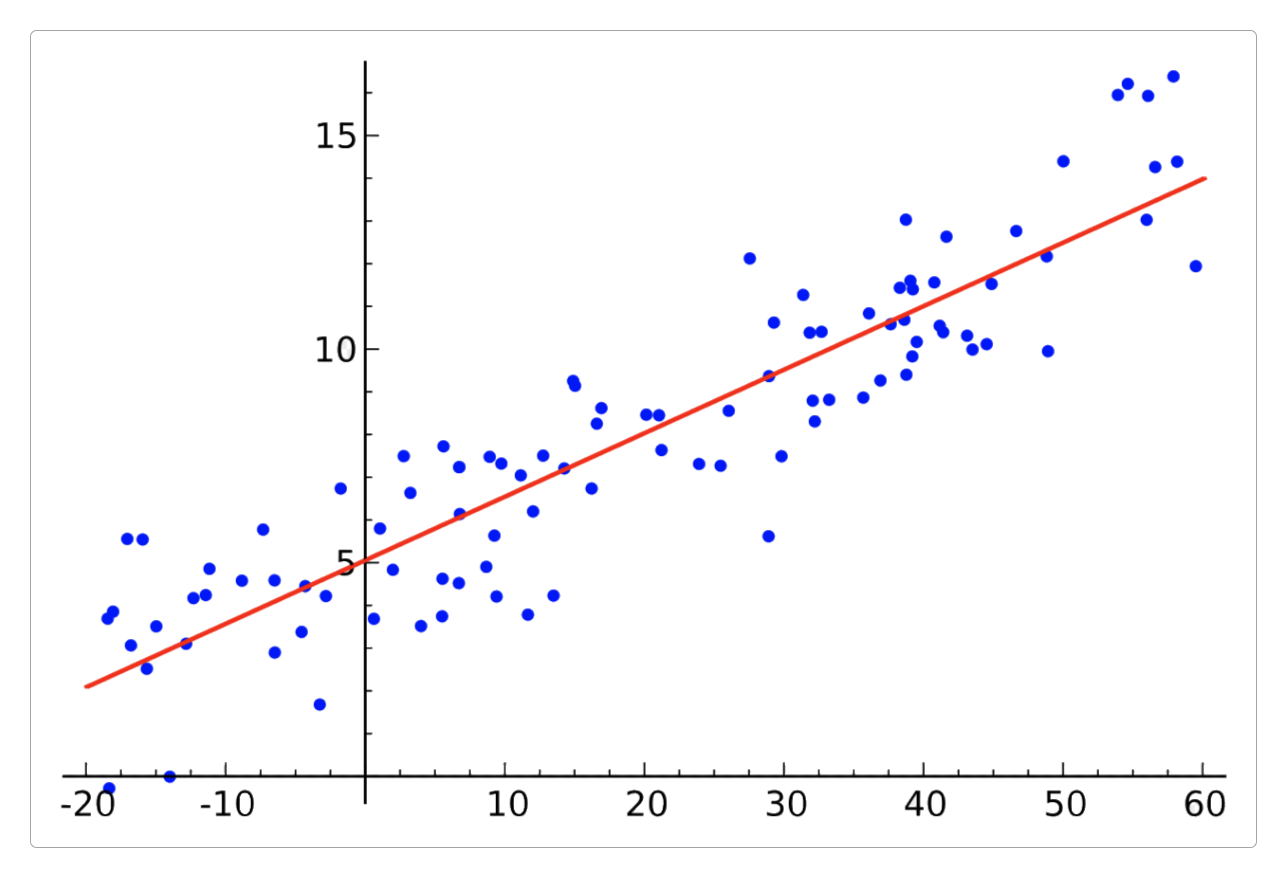
线性回归的一般形式是 $f (x) = k t + b$ ， $k 、 b$ 为待求的未知参数。

为了找到合适的 $k 、 b$ ，就要使殘差平方和最小，也就是 $R S S = M i n (\sum_{i = 1}^{n} (y_{i} - f (x_{i}))^{2}) = M i n (\sum_{i = 1}^{n} (y_{i} - (k \cdot x_{i} + b))^{2})$ 。

求解 $k$ 和 $b$ 的过程就是最小二乘法。

当线性回归方程中的变量很多的时候，直接通过方程求解的方式使用最小二乘法会非常麻烦，此时就可以利用线性代数来求解。

矩阵的基础运算法则如下。

向量： $a = (\begin{matrix} a_{1} \\ a_{2} \\ ⋮ \\ a_{n} \end{matrix}), | a^{2} | = \sum_{i = 1}^{n} a_{i}^{2} = a^{T} \cdot a$ 。
矩阵转秩： $X = (\begin{matrix} x_{11} & x_{12} \\ x_{21} & x_{22} \\ x_{31} & x_{32} \end{matrix}), X^{T} = (\begin{matrix} x_{11} & x_{21} & x_{31} \\ x_{12} & x_{22} & x_{32} \end{matrix})$ 。
矩阵乘法： $(\begin{matrix} 1 & 2 & 1 \\ 2 & 3 & 2 \end{matrix}) \cdot (\begin{matrix} 1 & 2 \\ 2 & 1 \\ 3 & 3 \end{matrix}) = (\begin{matrix} 8 & 7 \\ 10 & 11 \end{matrix})$ 。
逆矩阵： $A B = B A = E, B = A^{- 1}$ 。

用Python计算线性回归方程。

# 用Python计算线性回归方程
from numpy.linalg import inv
from numpy import dot
import pandas
import numpy as np

data = pandas.read_csv('data.csv')
arrs = np.array(data)
# print(arrs)
# 取出前三列
X1 = arrs[:, 0:3]
# 取出第四列
y = arrs[:, 3]
# 生成矩阵X
m, n = X1.shape
# 生成数据全为1的向量
b = np.ones(m)
# 拼接矩阵
X = np.c_[b, X1]
# print(X)
# 计算矩阵x的转秩
a = dot(dot(inv(dot(X.T, X)), X.T), y)
# 结果应该和最小二乘法计算的结果相同：y = 1.5 + 0.5 * x1 + 0.8 * x2 - 0.2 * x3
print(a)

感谢支持

更多内容，请移步《超级个体》。